Cách tốt nhất để tài giỏi là bắt bộ não rèn luyện hằng ngày
"Không có vấn đề nào không thể giải quyết được mà chỉ có những bài toán khó đương đầu". "Nếu chúng ta có thể dạy cho tay và chân, vì sao chúng ta không thể dạy cho bộ não?", thiên tài toán học Grigori Perelman nói về việc rèn luyện bộ não để giành được giải thưởng thiên niên kỷ của viện Clay trong một buổi phỏng vấn.
Cách tốt nhất để rèn luyện bộ não là gì? Dưới đây là ý kiến của một nhà khoa học trên quora.com, một trong những website hỏi đáp nổi tiếng nhất hiện nay.
Theo nhà nghiên cứu thần kinh học Tiberiu Tesileanu thuộc trung tâm sinh học điện toán học viện Flatiron (New York), chúng ta rèn luyện bộ não theo cùng một cách mà chúng ta rèn luyện cơ thể: tập luyện!
Nếu không có chủ đề nào mà bạn có hứng thú riêng thì hãy đọc rộng nhiều chủ đề. (Ảnh minh họa).
Theo đó, bạn cần học các chủ đề mà bạn hứng thú bằng cả 2 cách: đọc hoặc hỏi mọi người và thực hành vận dụng các chủ đề bằng cách giải bài tập (với môn toán, vật lý), viết (nếu bạn tính học văn học), soạn nhạc (với âm nhạc)...
Cũng cần ghi nhớ là, thỉnh thoảng bạn cần làm việc chăm chỉ để học một cái gì đó mà bạn không hứng thú, để giúp mình giải quyết vấn đề thật sự hấp dẫn bạn. Nếu không có chủ đề nào mà bạn có hứng thú riêng thì hãy đọc rộng nhiều chủ đề. Theo thời gian, bạn sẽ tìm được một số thứ để tập trung.
Việc mọi người tìm kiếm những con đường tắt hay lối tắt (shortcut) để học là rất phổ biến. Mọi người thường hỏi về một app thần kỳ có thể dạy bạn học toán nhanh hơn, cuốn sách kỳ diệu có thể dạy bất kỳ ai thành thạo nhiếp ảnh trong hai tuần, website phép màu dạy bạn thiết kế căn bản trong 10 phút… Vấn đề là: tất cả những thứ đó đều vớ vẩn.
Điều quan trọng nhất trong việc cải thiện bộ não không phải là bạn học từ sách nào mà là số lượng thực hành mà bạn thực hiện, và điều đó cần thời gian. Điều này cũng tương tự với thể thao: Bạn có thể đọc tất cả những gì bạn muốn về tennis, nhưng trước khi bạn cầm một cây vợt trong tay và đánh bóng hàng ngàn lần, bạn sẽ không quen với việc giỏi làm việc đó. Vì vậy, lần tới, khi đang cố gắng học một điều gì đó, hãy đảm bảo là bạn sẽ thực hành nó.

Khi đang cố gắng học một điều gì đó, hãy đảm bảo là bạn sẽ thực hành nó. (Ảnh: Telegraph).
Một xu hướng khác nổi lên gần đây là các bài tập thường bao gồm cả bối cảnh. Ví dụ, nhiều thập niên trước, một bài toán có thể chỉ là "tính tích phân" dưới đây:
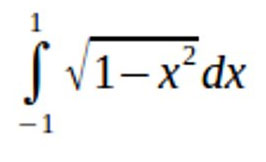
Ngày nay, bạn phải nghĩ ra một câu chuyện cho đề bài: "Ann muốn làm một tấm bảng bằng gỗ hình bán nguyệt để treo lên cửa phòng. Cô ấy muốn biết diện tích tấm bảng để tính được trọng lượng của nó. Bạn có thể giúp cô ấy được không?"
Điều này có vẻ là một ý tưởng hay: sinh viên học được cách làm thế nào để giải quyết các bài toán trong cuộc sống thực thay vì giải toán tích phân một cách máy móc. Vấn đề là sinh viên có thể mắc kẹt vào các chi tiết và kết thúc mà không học được gì. Thay vào đó, tốt hơn là nên chia nhỏ tiến trình học thành các bit nhỏ có thể quản lý được. Đó chính là lý do vì sao bạn học cách lấy tích phân của các hàm số tùy ý riêng rẽ với việc học cách quyết định hàm số nào có thể lấy tích phân.
Tương tự trong môn tennis, việc bạn cố gắng học tennis bằng cách chơi các trận đầy đủ ngay từ đầu không phải là một cách tốt. Trên thực tế, nếu bạn nhìn vào các tuyển thủ tennis giỏi nhất thế giới, họ vẫn tập luyện các cú đánh trái tay và thuận tay, serves-and-volleys (một kiểu chơi mà tay vợt sau khi giao bóng xong sẽ chạy ngay lên lưới với hy vọng đánh được cú kế tiếp), không phải lúc nào họ cũng chỉ tập chơi các trận đầy đủ.
Tóm lại: hãy sử dụng bộ não của mình, đó là cách bạn tập luyện nó. Đừng quên việc này sẽ mất thời gian và công sức và sẽ không có bất kỳ đường tắt nào trong thực tế.
Nhà toán học Grigori Perelman và giải Thiên Niên Kỷ
Grigori Perelman là nhà toán học người Nga sinh năm 1966 đã giành giải Thiên Niên Kỷ (Millennium Prize) của viện toán học Clay ở Mỹ với công trình chứng minh giả thuyết Poincaré.

Thiên tài toán học Grigori Perelman
Giả thuyết Poincaré (Poincaré Conjecture) là một trong bảy bài toán khó nhất của thiên niên kỷ thứ hai (1001-2000) được viện Clay trao giải thưởng 1 triệu USD/bài toán. Trong lĩnh vực topo đại số, giả thuyết Poincaré là một trong những thách thức toán học lớn nhất. Giả thuyết Poincaré rất phức tạp và khó hiểu với những người không học chuyên ngành topo có thể được mô tả lại một cách đơn giản như sau: tất cả các đa tạp ba chiều đóng và đơn liên (liên thông đơn giản, được kết nối đơn giản) đều có thể được biến đổi hình dạng và làm trơn thành các mặt cầu.
Đa tạp (manifold) là một khái niệm toán học mở rộng của đường và mặt phẳng trong không gian nhiều chiều. Ví dụ hình xuyến (torus) là một đa tạp 2 chiều, những vật có dạng khối lập phương, khối cầu là các đa tạp 3 chiều.

Đa tạp là một khái niệm toán học mở rộng của đường và mặt phẳng trong không gian nhiều chiều. (Ảnh: Bounded Rationality).
Đa tạp ba chiều đóng và đơn liên nói nôm na là những vật thể trừu tượng không có lỗ trống trong chúng, như bề mặt của một quả cầu trong bóng đá, bóng chày.
Theo GP, tất cả không gian ba chiều đóng và không có lỗ thủng (lỗ trống) đều có đặc trưng hình học giống nhau, không có sự phân biệt và được coi là duy nhất. Nói cách khác, không gian ba chiều khép kín không thủng là duy nhất. Giả thuyết GP trong không gian hai chiều đã được các nhà toán học chứng minh từ thế kỷ 19 còn GP trong không gian ba chiều được nhà toán học Pháp Henri Poincaré nêu ra năm 1904.
Năm 2003, Perelman đã chứng minh được GP đúng trong không gian ba chiều, trường hợp khó nhất của bài toán tổng quát trong không gian n chiều. Trước Perelman, đã có ba nhà toán học khác giành được giải thưởng Fields nhờ các công trình liên quan đến GP: chứng minh được GP đúng trong các trường hợp không gian nhiều hơn 3 chiều (n > 3) của Stephen Smale và Michel Friedman, cấu tạo của các đa tạp ba chiều gồm các phần đồng nhất và liên kết có điều kiện (một công trình có đóng góp quan trọng vào việc chứng minh GP) của William Thurston.
Công trình của Perelman có rất nhiều ý nghĩa trong toán học, giúp các nhà toán học có thêm hy vọng giải được những bài toán khó khác bằng phương pháp chứng minh của Perelman. Chứng minh giả thuyết Poincaré cũng rất quan trọng đối với lĩnh vực vật lý lý thuyết vì các phương trình Perelman sử dụng có nhiều điểm giống với phương trình tổng quát của thuyết tương đối, có thể giúp chúng ta khám phá thêm những hiểu biết mới về vũ trụ. Do đó, công trình của Perelman đã được tạp chí Science (một tạp chí khoa học nổi tiếng ở Mỹ) bình chọn là sự kiện đột phá của khoa học năm 2006, được chọn trao giải Fields-giải Nobel trong toán học năm 2006 và giải Thiên Niên Kỷ của viện Clay năm 2010 trị giá 1 triệu USD. Tuy vậy, Perelman đã từ chối cả hai giải thưởng danh giá này.
- Bí quyết để có bộ não khỏe mạnh
- Cách tốt nhất giúp trẻ phát triển khả năng ngôn ngữ
- Cách duy nhất để cứu sống điện thoại khi gặp nước
- Thời điểm tốt nhất để quan sát 5 hành tinh thẳng hàng ở Việt Nam
- Cách tốt nhất đảm bảo an toàn cho trẻ khi đi ô tô
- Những cách tốt nhất để phòng ngừa bệnh cúm
- Mách bạn những cách tốt nhất để loại bỏ thuốc trừ sâu, hóa chất độc hại trên rau củ
Y học - Sức khỏe
-

Phát hiện quái vật biển kỳ dị ở Trung Quốc
-

Vẫn thạch khác thiên thạch như thế nào?
-

Động đất là gì? Động đất được hình thành như thế nào?
-

Nguy cơ hải tượng long xâm chiếm vùng Amazon
-

Lý giải hiện tượng cầu vồng lửa
-

Kali xyanua là gì?
Đời sống
-

Ukraine: “Thảm họa Chernobyl” thứ hai
-

Lần đầu tiên trên thế giới “làm sống lại” tim ếch đóng băng
-

Bắc Kinh cấm hút thuốc trong taxi
-

NASA khởi động dự án nghiên cứu biến đổi khí hậu
-

Giải mã căn bệnh "da đàn hồi" cực hiếm trên thế giới
-

Lo ngại đột biến nguy hiểm hơn của biến chủng Delta