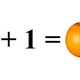Logic học – Sợi dây liên kết giữa toán học và văn học
1) Phép phản chứng:
Trong toán học phép suy luận phản chứng đã giúp chứng minh rất nhiều bài toán, tính chất, định lý… Ví dụ như: chứng minh “không có số nguyên tố lớn nhất”
Giả sử rằng có số nguyên tố n lớn nhất. Khi đó ta xét số sau đây: N=n!+1 (N>n). Dễ thấy rằng số N không chia hết cho tất cả các số từ 2->n (trong đó bao gồm tất cả các số nguyên tố) => N là số nguyên tố. Điều này vô lý vì theo giả sử số n là số nguyên tố lớn nhất.
=> Không có số nguyên tố lớn nhất.
 Để nói về suy luận phản chứng trong văn, chúng ta sẽ bắt đầu từ câu truyện cười “Mâu – thuẫn”:
Để nói về suy luận phản chứng trong văn, chúng ta sẽ bắt đầu từ câu truyện cười “Mâu – thuẫn”:
Có một người nước Sở làm nghề vừa bán mộc, bán giáo. Ai hỏi mua mộc thì anh ta khoe rằng: “Mộc này thật chắc, không gì đâm thủng”. Ai hỏi mua giáo thì anh ta khoe rằng: “Giáo này thật sắc, gì đâm cũng thủng”. Có người nghe được vậy, hỏi rằng “Thế bây giờ lấy giáo của bác đâm vào mộc của bác thì thế nào?”. Anh ta không đáp ra làm sao được (Logic học phổ thông – Hoàng Chúng).
Chính hai câu nói mang tính “quảng cáo” đã gây bất lợi cho anh ta. Thật vậy:
+ Nếu giả sử câu nói thứ nhất đúng thì giáo anh ta bán sẽ không đâm thủng mộc anh ta bán => mâu thuẫn với câu nói thứ hai => câu nói đầu tiên sai => mộc không chắc như anh quảng cáo.
+ Nếu giả sử câu nói thứ hai đúng thì giáo anh ta bán sẽ đâm thủng mộc anh ta bán => mâu thuẫn với câu nói thứ nhất => câu nói thứ hai sai => giáo không sắc như anh quảng cáo.
Trong vấn đề bình luận văn học, suy luận phản chứng tạo ra một nét riêng, đặc sắc, tạo sự bất ngờ, thú vị cho người đọc. Ví dụ như, hãy bình luận câu sau “Tiền bạc đem đến hạnh phúc”.
Chúng ta đọc lời bình sau: Có lẽ quan điểm trên là đúng. Thật đơn giản. Có tiền mới làm được việc, không tiền thì chẳng làm được gì cả. Những người ham mê ca nhạc, muốn vào xem nhạc cũng phải có tiền mua vé, thiếu một xu thì không thể xem được ca sĩ mà mình hâm mộ. Khi có tiền, người ta sẽ ăn sung mặc sướng. Nếu thiếu tiền thì việc kiếm miếng cơm ăn qua bữa cũng quý lắm rồi, còn sức đâu mà nghĩ đến chuyện hạnh phúc hay không.
Tuy nhiên, việc lý luận trên đã đủ sức thuyết phục chưa?
Có những người chỉ cần nhìn thấy được thần tượng của mình là vui và hạnh phúc lắm rồi, cần chi đến việc bắt buộc kiếm một số tiền khá lớn để mua vé xem ca sĩ nổi tiếng. Đó có chăng chỉ là sự đòi hỏi quá mức của bản thân đối với hoàn cảnh thực tế. Ngay cả việc ăn sung mặc sướng cũng vậy. Có phải chăng những người có tiền ăn sung mặc sướng là hạnh phúc? Ăn là điều tất yếu của cơ thể. Tuy nhiên, nếu ăn không đúng, cũng gây ra biết bao nhiêu căn bệnh cho cơ thể, nhất là trong thời điểm vệ sinh an toàn thực phẩm đang được cảnh báo nhiều như hiện nay. Còn mặc? Nếu có tiền mà mặc quá bóng bẩy, se sua, không thích hợp vóc dáng thì cũng chỉ để thiên hạ nhìn thấy mà cười. Như vậy, tiền bạc không nhất thiết đã đem lại hạnh phúc”.
Qua bài bình luận trên, người viết đã rất khéo léo lật ngược vấn đề, để cho thấy được câu nói “Tiền bạc đem đến hạnh phúc” là sai.
2) Phép quy nạp và phép diễn dịch:
Trong toán học, phép diễn dịch rất thường được sử dụng trong các lý luận, cấu trúc thường được sử dụng như sau: 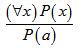
VD: Xét định lý: “Mọi số tự nhiên có chữ số tận cùng là 0 hoặc 5 thì chia hết 5”. Ta có số 125 có tận cùng là 5 => 125 chia hết cho 5.
Suy luận quy nạp trong toán học nghĩa là đi từ các riêng, cụ thể để kết luận cái chung, tổng quát. Với phương pháp quy nạp, người ta đã chứng minh được nhiều định lý, công thức, đẳng thức, bất đẳng thức …
VD:
a) 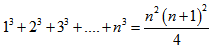 với mọi số tự nhiên n ³1
với mọi số tự nhiên n ³1
b) (Bất đẳng thức Bernuli): chứng minh với mọi x >- 1, x ¹ 0 và với mọi số tự nhiên n ³ 2 ta có bất đẳng thức sau đúng: (1+x)n>1+nx
Trong ví dụ trên, để chứng minh được người ta sử dụng phương pháp quy nạp hoàn toàn nghĩa là cũng đi từ cụ thể nhưng chứng minh được cho mọi trường hợp cụ thể, nên chắc chắn sẽ đúng với tổng quát. Với quy nạp không hoàn, nghĩa là chỉ một số trường hợp mà đúc kết thành một tính chất tổng quát, thì chưa chắc đã thu được mệnh đề đúng.
VD: Nhà toán học Pháp Fermat đã xét dãy số 5, 17, 257, 65537,… với số hạng tổng quát 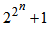 . Ông nhận thấy rằng, 4 số hạng đã viết ở trên tương ứng với n=1,2,3,4… là những số nguyên tố. Ông giả định rằng các số tiếp theo cũng là những số nguyên tố. Tuy không chứng minh được nhưng ông vẫn cho rằng giả thuyết của mình là đúng. Nhưng Euler đã tìm thấy rằng ngay số hạng tiếp theo ứng với n=5: 232+1 không phải là số nguyên tố vì chia hết cho 614.
. Ông nhận thấy rằng, 4 số hạng đã viết ở trên tương ứng với n=1,2,3,4… là những số nguyên tố. Ông giả định rằng các số tiếp theo cũng là những số nguyên tố. Tuy không chứng minh được nhưng ông vẫn cho rằng giả thuyết của mình là đúng. Nhưng Euler đã tìm thấy rằng ngay số hạng tiếp theo ứng với n=5: 232+1 không phải là số nguyên tố vì chia hết cho 614.
Phép suy luận quy nạp và phép diễn dịch cũng có trong văn học.
VD: truyện “thầy bói xem voi”, các thầy bói mù, mỗi người chỉ sờ vào một bộ phận con voi (vòi – chân – tai – đuôi) (cái riêng), mà kết luận liền là con voi chỉ giống như (đĩa – cột nhà – quạt – chổi) (đi đến kết luận chung). Các thầy bói “thấy cây mà không thấy rừng”, nhìn phiến diện, lập luận bằng phép quy nạp không hoàn toàn. Nên dẫn đến phán đoán về con voi là sai.
Hay trong câu ca dao Việt Nam, một thầy bói “phán”:
“Số cô có mẹ có cha
Mẹ cô đàn bà cha cô đàn ông
Số cô có vợ có chồng
Sinh con đầu lỏng chẳng gái thì trai”.
Trong trường hợp này thầy bói đã đi từ một mệnh đề luôn đúng “ai là người cũng có mẹ có cha”, vì cô là người nên cô cũng có mẹ có cha. Đó chính là phép diễn dịch. Thành ra, thầy bói trong trường hợp thứ này nói điều gì cũng đúng và đồng thời những điều đã nói ai… cũng biết.
Tóm lại, thế giới toán học và văn học tuy khác nhau nhưng lại có những nét tương đồng.
Hỏi đáp Khoa học
-

Trái đất đang nằm ở điểm xa nhất so với Mặt trời, vì sao nhiệt độ mùa hè năm nay vẫn ở mức cao kỷ lục?
-

Tàu Mặt trăng của Nga chụp ảnh từ ngoài không gian
-

Top 11 phát minh làm rạng danh người Việt
-

Chiến tranh đà điểu tại xứ sở chuột túi
-

Tại sao một số lông trên cơ thể bạn có thể mọc dài tới mức vô lý?
-

Loài chim bồ câu khổng lồ bất ngờ xuất hiện sau 140 năm "mất tích"